これは何？

EUF(Equality Logic with Uninterpreted Function)用のSMTソルバを、SATソルバは既知のものとして作ってみた話です。

なんでやろうと思ったの？

前からAlloy(https://alloytools.org/)のような、SATを利用して何かを作るということに興味があったからです。また、ChatGPTを始めとするLLM技術の発達を見ていて、LLMにもっと論理性を外部から与えられないかということは考えており、SATとLLMの間にループを作って何かを解く、ということができないかということは考えていました。

ただ、それ以前の段階としてそもそもSATの用例として基本的なSMTすら実はよくわかってないなと思い、とりあえず簡単そうなSMTの自作から始めてみようと思いました。

EUFって？

EUFは(Equality Logic with Uninterpreted Functions)のことで、変数と関数記号たちで作った項を=でつないだものたちを基本的な命題として使える論理体系です。なんとなくでわかりそうなので例だけ出してお茶を濁そうと思います。正確なところはこちらをご欄ください: https://www21.in.tum.de/teaching/sar/SS20/6.pdf

たとえば、a,b,cを変数として「not (a = b and b = c) or a = c」は関数記号のあらわれないEUFの式です。ちなみにこの式は日本語的には「『a=bかつb=c』ならばa=c」で、この論理で要請されている等式の推移律を使えば、構文的に(syntacticに)真であることがわかります。式の(論理学用語で言うところの)構造は、各変数が走る集合Xを1つ定め、各変数にその集合Xの値を割り当てることで定まります。今回の例であれば、例えば集合として自然数全体を取り、a=0, b=1, c=2として意味を考えることができます。このとき、「a=b」が偽なので「a = b and b = c」も偽となり、「not (a = b and b = c)」は真となるので、先の式は全体として真になります。なので、今回とった構造「集合として自然数全体、変数割り当てとしてa=0, b=1, c=2」のもとで、この式は真であることがわかります。この式に関して言えば、どんな解釈を持ってきてもこの式は真になります*1。

さらに関数記号を使った式も考えられます。例えば上の記事で紹介されている例ですが、a,bを変数とし、fを2変数関数の記号として、「f(a, b)=a and f(f(a, b), b) ≠ a」という式もEUFの式です。ただし≠は、その等式にnotをつけたものの略記です。人間的な証明になりますが、これは充足不能(unsatisfiable)であることがわかります。実際、「f(a, b)=a」を使えば「f(f(a, b), b) = f(a, b)」となることがわかります。これと「f(f(a, b), b) ≠ a」を組み合わせると「f(a, b)≠a」となりますが、これは「f(a, b)=a」と矛盾するからです。この式の構造は、先のように集合と各変数の割り当ての他に、各関数への割り当てをすることにより定まります。今回はfが2変数関数の記号なので、これにX×X→Xの型の関数を割り当てることになります。例えば「集合として自然数全体、変数割り当てとしてa=0, b=42、関数への割り当てとしてf(x, y) = x+y」という構造を考えます。すると、「f(a, b) = f(0, 42) = 0 + 42 = 42」となりますが、「a=42」なので「f(a, b)=a」がなりたたず偽になります。よって、この式はこの解釈のもとで偽です。この式に関しては、どんな解釈を持ってきてものこの式は偽になります。

注意点として、EUFでは(論理学用語で言うところの)理論はありません。つまり、関数記号たちについて、それが満たすべき公理を要求することができません。なので、fが可換な関数の記号であることを期待していたとしても、個別の変数について「f(a, b)=f(b, a)がなりたっていて、f(a, c) = f(c, a)がなりたっていて…」というのを論理式のレベルで書くことはできますが、「f(x, y)には可換な関数だけが割り当たるようにして、そのもとでこの式を解釈してね」というように構造のレベルで非可換な関数が割り当てられるのを弾くことはできません。

EUF、何の役に立つの

まず大前提として、後述するようにコンピュータで解きやすい*2、つまりvalidityが検査しやすいというのはあります。どんなに記述能力が高く、いろいろな問題を帰着できたとしても、その問題がコンピュータで検査しなければ、その論理を使って何か役立つプロダクトを作ることはできません。

このもとで、EUFを使って2つのプログラムの等価性の検査に使うという事例が紹介されています*3。 https://www.csa.iisc.ac.in/~deepakd/logic-2021/EUF.pdf

1つ目のプログラムとして

|| u1 := (x1 + y1); T2: u2 := (x2 + y2); T3: z := u1 * u2; ||< を考え、2つ目として || z := (x1 + y1) * (x2 + y2); ||< を考えます。1つ目と2つ目の等価性を調べるには、これらの代入たちを等式と見做し、「u1=(x1+y1) and u2=(x2+y2) and z=u1u2 implies z=(x1 + y1)(x2+y2)」というEUFの論理式を考えます。EUFでは実際+と*がどういう関数かはよくわかりませんが、どういう関数かわからないまま(uninterpreted!)でもこの論理式がvalidであることはわかります。これによって、2つのプログラムが等価であることがわかります。

等価性だけだとこんなの当たり前やんとなりますが、もうちょっと非自明な性質、例えば「このループを実行している間、変数たちはこういう性質を満たし続けているはずだ」というような性質を調べたいというのもプログラム検証のテーマで、そういったものにも使われているはずです。適当に見つけたこの論文( Invariant Checking of NRA Transition Systems via Incremental Reduction to LRA with EUF | SpringerLink )なんかはIC3とEUFと言っているので多分そんな感じだと思います。

EUFについてのアルゴリズム

先程EUFはコンピュータで解きやすいと言いましたが、実際リテラル(a=bの形の式か、またはa≠bの形の式をandでつないだもの)の充足可能性を効率良く判定することができます。

ひとまずとても簡単な特殊ケースとして、そのリテラルに関数記号があらわれないとします。たとえば、a,b,c,d,eを変数記号として「a=b and b=c and d=e and e≠a」を考えます。この充足可能性を確認するには、まず≠の部分は忘れて、等式だけに注目します。等式で結ばれているもの同士をつないだ無向グラフを考えると、a,b,cという連結成分とc,dという連結成分ができます。等式で結ばれているのですから、推移律より同じ連結成分に属するものは同じ値が割り当てられる必要があります。反対に、違う連結成分同士のものは違うものを割り当てても構わず、等式に縛られる制約はこれが全てです。あとは、≠を思い出せばよく、≠によってある連結成分の中の異なる2要素が結ばれているかどうかを確認すればよいです。もしも結ばれているならば、それは連結成分の作り方に矛盾するので充足不能となります。もしも結ばれていないならば、全ての異なる連結成分に違う値を割り当てればそれでリテラルの全ての制約が満足され、充足可能となります。このように、EUFのリテラルは変数たちについて無向グラフを作るだけで判定することができます。実際には、Union-Find木をつかってもっと効率良くします。

一般の関数記号を含む論理式についても、そこで考えればよい論理式を全部列挙してしまえば上と同じ方法で検査ができます。大雑把に言えばそのようなアイデアで、細かい話は https://www21.in.tum.de/teaching/sar/SS20/6.pdf を見てください。

では、リテラルとは限らないEUF論理式について判定をするにはどうするのか？というと、そこでSATソルバを利用することができます。

すごい雑なSMTソルバ

SATソルバは、命題論理の論理式の判定が効率的にできる装置です。他方、上のアルゴリズムはEUFのリテラルに限って判定が効率的にできる装置でした。この2つを組み合わせることで、一般のEUFの論理式についての判定を高速に行うことができます。

一般論を書くよりは例を示したほうが早そうなので例で示します。最初の「not (a = b and b = c) or a = c」を解いてみます。

まず、基本の論理式たちを、等式としての性質は忘れて命題論理の基本命題と思いなおし、命題論理の論理式に変換します。例えば、a=bという等式を、『a=b』という1文字だと思いなおします。すると、『a = b』『b = c』『a = c』を基本的な命題とした命題論理の論理式「not (『a = b』 and 『b = c』) or 『a = c』」が出来上がります。
出来上がった命題論理をSATソルバに食わせます。今回は『a=b』にTrue、『b=c』にFalse、『a=c』にFalseという割り当てが返ってきたとします。
最初に忘れた等式としての性質を思い出し、「a=b」がTrue、「b=c」がFalse、「a=c」がFalseということが実際に起こりうるかを調べます(これらは命題論理の命題『a=b』ではなくEUFの命題「a=b」であることに注意してください)。この確認は、「a=b and b≠c and a≠c」というEUFのリテラルの判定によってできます。これは充足不能です。これで、命題論理ぐらい大雑把に見れば充足可能だけど、EUFで見ると充足不能で、SATソルバが教えてくれた割り当ては「偽物」だったことがわかります。SAT/SMT界隈でそう言うかは知りませんが、プログラム検証の界隈ではこのような「大雑把に見れば正解だけど元の粒度で見ると間違い」という解のことをspurious(それっぽい偽物)と言ったりします。
なので、今度はSATソルバに、「さっきの解じゃないやつで何か他の割り当てある？」と聞いてみることにします。これには、「not (『a = b』 and 『b = c』) or 『a = c』」にさらに「『a=b』 and not『b=c』 and not『a=c』」という式をandでくっつけ、同じ解が出てくることを明示的に禁止します。その結果今度は、『a=b』、『b=c』、『a=c』がすべてTrueという結果がSATソルバから返ってきたとします。
また等式としての性質を思い出し、今度は「a=b and b=c and a=c」というEUFリテラルが充足可能かを調べます。すると今度は充足可能だとわかります。なので、先のSATソルバが返してきた答えは、EUFの論理式の答えとしても使える「本物」でした。これで、最初のEUF論理式「not (『a = b』 and 『b = c』) or 『a = c』」は充足可能であり、a=b=cとなるようにすればよい、ということがわかりました。

今回は充足可能というのが答えでしたが、充足不能の場合はSATソルバが「充足不能」という答えを返してきます。等式としての性質を忘れた大雑把な見方ですら充足不能であれば、EUFの論理式としても充足不能ということになるので、これでどちらの場合も判定ができることになります。

このように、SATソルバと、リテラルの判定ができるような論理(今回はEUF)のリテラル判定機を組み合わせることで、その論理の式を判定する機械を作ることができます。このような機械をSMTソルバといいます。

プログラムをかくぞ

おおまかな課題はこんなかんじになります:

命題論理の論理式のためのデータ構造をつくる
SATソルバを組込む(今回はminisatというのを使います。もっといいのあるかも)
EUFの論理式のためのデータ構造をつくる
命題論理の論理式 ←→ EUFの論理式の相互変換をつくる
EUFリテラルの判定をつくる: EUFの関数記号にいい感じに対応したUnion-Find木をつくる(先の論文参照)
テストライブラリをなんか持ってくる
SMTソルバのループ構造をつくる

ChatGPTにモチベをあげてもらう

最近疲れてしまってまとまった時間がとれないので、ChatGPTにマネージャと相談相手を任せることにしました。

本当はそこを怠ってはいけないのですが、「知りたいこと→検索ワード」という変換をする手間は省けてがっと調べられるので、「あー、これ調べないといけないんだけどどう調べたもんかな、あー眠くなってきた寝よ…」ということは減って随分快適にはなりました。堕落とも言う気がしておりちょっと怖いです。

喋るラバーダック

たすかる～

愚痴も言える

報告なんかしたりすると楽しい

「素晴しい進歩です！」みたいなの、しょうもないといえばしょうもないんですが、しょうもなくても言ってくれることの大事さというのはリングフィットアドベンチャーで学びました。

愚痴も言える(2)

しょうもない質問

こまかい命名とかも人には相談しづらいけどChatGPT相手だと気軽に聞けますね

まあlessは思い付くけど他にあるのかなとか…

微妙に検索するのが面倒な質問

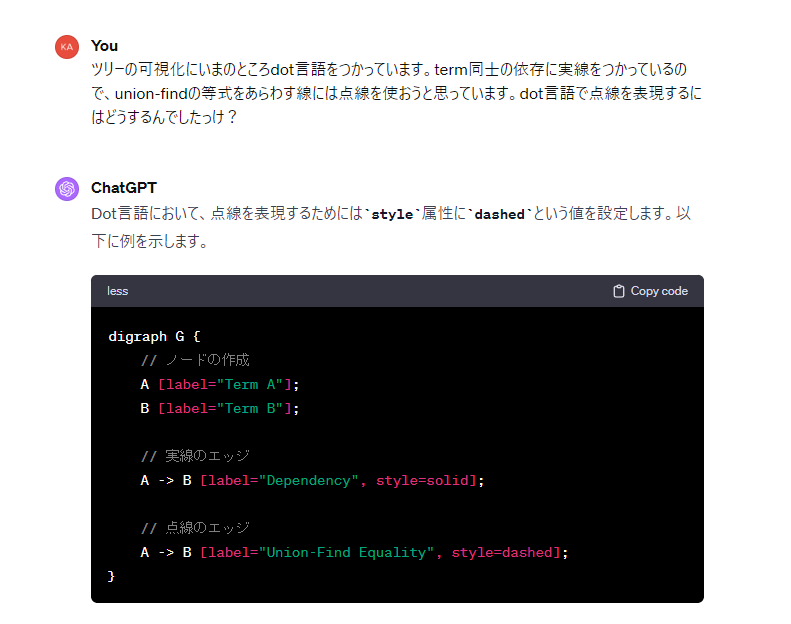dot言語とか微妙にぐぐるのが面倒なので

decltypeが出てこなかったのですが、「あー値から型を作ってくれるあれ～」だと検索できないので助かりました

細かいエディタの設定みたいなのも検索かけるとノイズが多くて…

プログラミング技法の相談

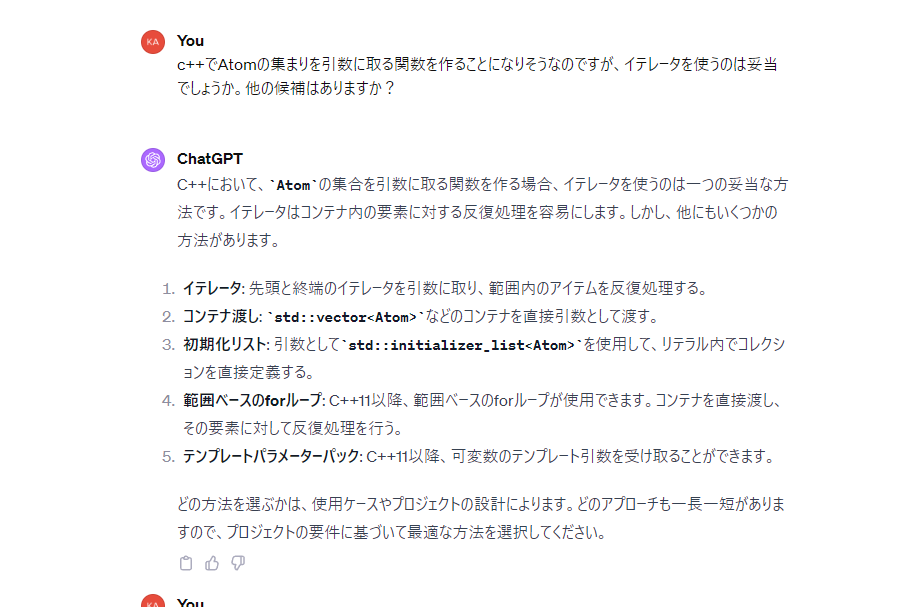一人で考えるとあんまり手段思いつかなかったりするのでいろいろ言ってくれるのは助かりますね

できたー

記事の最初にあげたような例が解けるようになり、次のようなテストがまわります。


TEST(EufTest, EufSolve){
    // https://www21.in.tum.de/teaching/sar/SS20/6.pdf
    std::vector<EufAtom> atoms;
    auto a = EufTerm(EufSymbol::MakeAtom("a"));
    auto b = EufTerm(EufSymbol::MakeAtom("b"));
    auto f = EufSymbol::MakeFunction("f", 2);
    auto fab = f.Apply2(a, b);
    auto ffabb = f.Apply2(fab, b);

    auto form1 = EufFormula::MakeAtom({true, fab, a});
    auto form2 = EufFormula::MakeAtom({false, ffabb, a});

    auto form = EufFormula::MakeAnd(form1, form2);
    
    auto model = EufSolve(*form.get());

    for(auto [k, v]: model.assignment){
        std::cout << k.left.Print() << (k.equality ? "==" : "!=") << k.right.Print() << "!!" << v << std::endl;
    }
    ASSERT_FALSE(model.satisfiable);
    

}

TEST(EufTest, EufSolve2){
    // https://www21.in.tum.de/teaching/sar/SS20/6.pdf
    std::vector<EufAtom> atoms;
    auto a = EufTerm(EufSymbol::MakeAtom("a"));
    auto b = EufTerm(EufSymbol::MakeAtom("b"));
    auto c = EufTerm(EufSymbol::MakeAtom("c"));
    auto f = EufSymbol::MakeFunction("f", 1);
    auto g = EufSymbol::MakeFunction("g", 2);
    auto fa = f.Apply1(a);
    auto gfab = g.Apply2(fa, b);
    auto fc = f.Apply1(c);
    auto gfca = g.Apply2(fc, a);

    auto form1 = EufFormula::MakeAtom({true, a, b});
    auto form2 = EufFormula::MakeAtom({true, b, c});
    auto form3 = EufFormula::MakeAtom({true, gfab, gfca});
    auto form4 = EufFormula::MakeAtom({false, fa, b});

    auto form = EufFormula::MakeAnd(form1, form2);
    form = EufFormula::MakeAnd(form, form3);
    form = EufFormula::MakeAnd(form, form4);
    
    auto model = EufSolve(*form.get());

    for(auto [k, v]: model.assignment){
        std::cout << k.left.Print() << (k.equality ? "==" : "!=") << k.right.Print() << "!!" << v << std::endl;
    }
    ASSERT_TRUE(model.satisfiable);
    

}

これからどうする？とりあえず1個SMTは作ってみることができたので、他の理論(例えばbitvectorとか)に行ってみるもよし、CTF界隈でSMTが使われてるというのを聞いているので実際どんな風に使っているのか覗きに行くもよし、最初の目標どおりAlloyを見にいくもよしで楽しそうですね。

*1:健全なのでそれはそう

*2:「解きやすい」と言うと真っ当な感覚を持ったプログラマは精々2乗オーダーぐらいかなと思い浮かべるかと思いますが、プログラム検証界隈は割合夢見がちな問題を扱っているので、decidableぐらいで全然喜びます。

*3:プログラム検査の話でしばしば感じることですが、「これ解くんだったらSMT使わんでも専用のアルゴリズム使ったほうがええやろ」ということはあります…なるほどという例にはまだ出会えていませんが、実はこういう簡単なものを積み重ねれば役に立つものができる、ということもあるのかもしれません

ashiato45の日記

EUF上の簡易SMTソルバを作ったりしていた